「すだれ算」ってご存知ですか?
すだれのように計算を下に伸ばしながら、簡単に素因数分解したり、最大公約数と最小公倍数を求めたりすることができる計算法です。
小学生でもできる作業のようなものなのですが、意外とこれが知られていないんですよね。
私も高校で初めて知りました。
そんな存在感が薄めのすだれ算…会得すれば問題を解くスピードがぐんと上がる優れものです。
今回は、小学生にも分かりやすいように初歩的なことから説明します。
ある程度数学用語が分かる中高生は、用語の説明は飛ばしても構いません。
素数と素因数分解について

すだれ算は主に最大公約数と最小公倍数を求める方法として使われるのですが、素因数分解もできます。
まずは、素数と素因数分解について大まかに説明したいと思います。
素数とは
まずは素数について少し説明します。
例えば、「12」という数は
・1×12
・2×6
・3×4
の三通りに分解することができます。
ここで出てきた「6」は
・1×6
・2×3
の二通りに、
「4」も
・1×4
・2×2
の二通りに分解することができます。
しかし、「2」と「3」は「1×2」「1×3」というように、「1×その数」の一通りにしか分解することができません。
この「1×その数」にしか分解できない数を「素数」と言います。これ以上割れない数ですね。
ちなみに「1」はどうなの?と思った方も多いと思いますが、1は素数に入りません。
ややこしいですが、とても大事なことなので覚えておきましょう。
素因数分解とは
素因数分解は、ある数を素数だけの掛け算に直すことです。
もうこれ以上分解できないというところまで分解します。
試しに30をa×bという形に分解してみましょう。
- 2×15
- 3×10
- 5×6
の三通りが出てきたと思います。
どれでもOKです。
そして、ここからさらに細かく分解していきます。
a×b×cの形にしてみましょう。
①の場合、15は「3×5」に分解することができます。
②の場合、10は「2×5」に分解することができます。
③の場合、6は「2×3」に分解することができます。
①~③、どの方法で分解しても「2×3×5」になるはずです。
2も3も5もこれ以上割ることができない素数なので、これで素因数分解は完了です。
すだれ算で素因数分解

いよいよすだれ算に入りますが、形が違うだけで内容は先ほどやった分解と同じです。
ただ、すだれ算は字におこしながら順番に分解するので、頭で計算するよりも早くて正確です。
先ほどと同じ例題で説明します。30を素因数分解してみましょう。
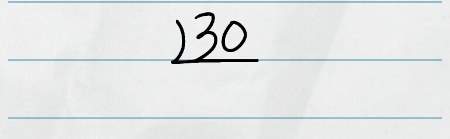
まずは素因数分解する数字を書いて、割り算の筆算の上下を反対にしたような線を引きます。

次に、素数で割ります。素数なら何でもいいですが、できるだけ小さい数から順番に割った方が良いでしょう。
割る数は、普通の割り算の筆算と同じように左側に。計算の答えは下に続いていきます。
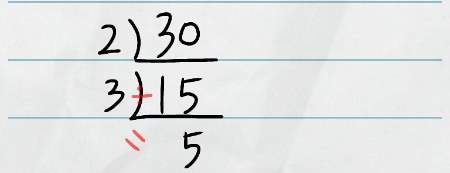
下に出た計算の答えを、さらに素数で割っていきます。
大きな数の場合は、計算の答えが素数になるまで同じ作業を繰り返して下に伸ばしていきます。

今回は二段で終了しました。結果は、赤丸がついている数字です。
30を、2と3と5に分けることができました。式にすると30=2×3×5 になります。
ポイントは、必ず素数で割ることと、素数になるまで割り算を続けることです。
当たり前じゃん!と思うかも知れませんが、全ての数が素数になる前に計算をやめてしまうミスは結構あります。
急いでいると、「21」とかを素数と勘違いして「分解し終わった!」という気になってしまうことが多々ありますのでご注意を。
最大公約数・最小公倍数について

続いて最大公約数と最小公倍数について説明します。
小中学校で習うと思いますが、時間が経つと案外定義があやふやになってくるので今一度確認してみましょう。
約数と倍数
約数とは「割り切ることができる数」のことを言います。
例えば、「6」という数は1・2・3・6で割ることができます。なので、6の約数は1・2・3・6になります。
倍数とは、ある数を自然数倍した数のことです。
これは簡単で、例えば「2」という数を2倍・3倍・4倍・5倍…した数、すなわち4・6・8・10などは2の倍数になります。
約数と違い、倍数は無限に存在します。
公約数・最大公約数とは
公約数とは、「2つ以上の自然数に共通な約数」のことです。
例えば、「12」と「6」の公約数を求めるとします。
12の約数は1・2・3・4・6・12で、6の約数は1・2・3・6です。
12と6の約数の中で、共通するのは1・2・3・6です。これらの数は全て、12と6を割り切ることができます。
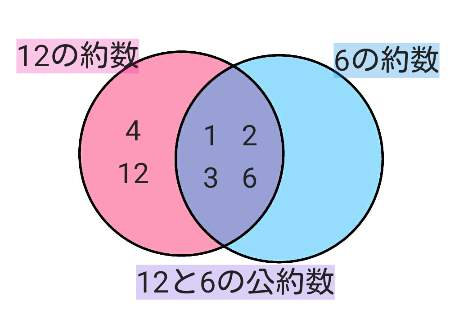
よって、12と6の公約数は1・2・3・6になります。
ちなみに、「2つ以上の自然数」なので3個でも4個でもいけます。
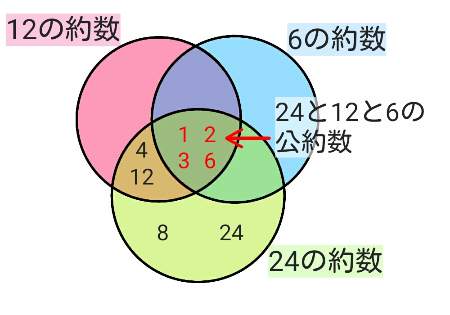
続いて最大公約数ですが、これは文字の通りで、いくつかある公約数の中で最も大きい数のことを指します。
先ほど求めた「12と6の公約数」は1・2・3・6。
この中で最も大きい数は6なので、「12と6の最大公約数」は6となります。
公倍数・最小公倍数とは
公倍数とは、「2つ以上の自然数に共通な倍数」のことです。
こちらも公約数より簡単です。例えば、「4」と「6」の公倍数を求めるとします。
4の倍数は4・8・12・16・20・24…と続き、6の倍数は6・12・18・24・30…と続きます。
それぞれの倍数の中で共通する数は「12」や「24」など。これらが「4と6の公倍数」となります。
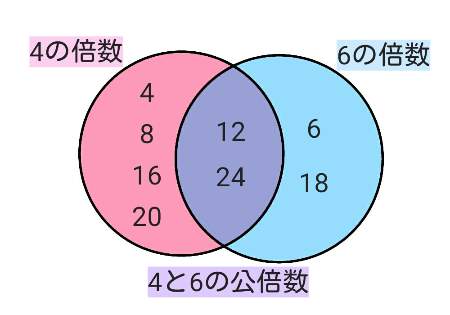
こちらも、対象となる数がたくさんある場合もあります。
続いて最小公倍数ですが、こちらも文字の通り、無限に存在する公倍数の中で最も小さい数のことを指します。
先ほど求めた「4と6の公倍数」の中で最も小さい数は12なので、「4と6の最小公倍数」は12となります。
最大公約数と最小公倍数の特徴
最大公約数と最小公倍数には大きな特徴があるので、覚えておいてほしいと思います。
まず最大公約数ですが、「公約数は最大公約数の約数となる」ということを覚えておきましょう。
約数約数となんのこっちゃ…と思うかも知れませんが、要するに、一つだけ存在する最大公約数さえ求めれば、いくつか存在する公約数を全て簡単に求めることができるのです。
「12と6の最大公約数」は6。
「6の約数」は1・2・3・6。
つまり、「12と6の公約数」は1・2・3・6 と、こんな感じです。
次に最小公倍数ですが、「公倍数は最小公倍数の倍数である」ことを覚えておきましょう。
こちらも倍数倍数と混乱しますが、最小公倍数さえ求めれば、後は適当に数を掛けるだけで永遠に公倍数を求めることができるのです。
「4と6の最小公倍数」は12。
「12の倍数」は12・24・36・48…
つまり、「4と6の公倍数」は12・24・36・48…と続くことが分かります。
公約数の求め方も公倍数の求め方も、例のように小さい数だと「回りくどいなあ」と思うかも知れませんが、数が大きくなると、公約数や公倍数を求めるのは結構面倒になってきます。
すだれ算で最大公約数と最小公倍数を求める

数学で最大公約数や最小公倍数を求めなくてはならない場面に遭遇した時、あなたはどうしますか?
丁寧に公約数や公倍数をノートやテスト用紙の隅に並べていくのもアリですが、数が大きくなると最大公約数も最小公倍数もなかなか出てこないので、かなりのタイムロスになってしまいます。
そんな時、すだれ算を使えば素早く正確に最大公約数や最小公倍数を求めることができますし、その答えを使えば先ほど説明したように、複数の公約数と公倍数を求めることもできます。
基本のすだれ算
見た目はちょっと特殊ですが、やっていることは「ひたすら簡単な割り算を繰り返し」行っているだけです。
では、6と12の最大公約数をすだれ算で求めてみます。
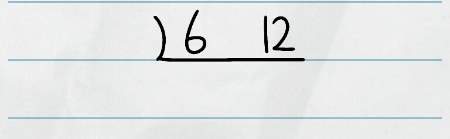
まずは6と12を並べ、割り算の筆算と上下反対の線を引きます。
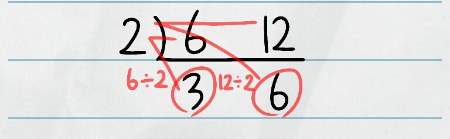
6と12はどちらも2で割り切れるので、割り算の筆算のように左側に2をつけます。
線の下にはそれぞれの数を2で割った結果を記入します。
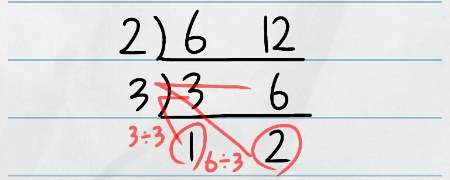
先ほどの割り算で出た3と6はどちらも3で割り切れるのでさらに計算を続けます。
この時、「2」「3」と分けずにいきなり「6」で割ってもOKですが、数が大きくなるとややこしくなるので、心配な場合は素数で割ることをお勧めします。
ここで出た1と2はもうこれ以上割ることができないので、すだれ算はここで終了です。

完成したすだれ算の左側の数を掛けると、二つの数の最大公約数になります。

最小公倍数は、L字型になっている赤丸部分の数を掛けると求めることができます。
慣れればとても簡単に計算することができます。
3つの数のすだれ算
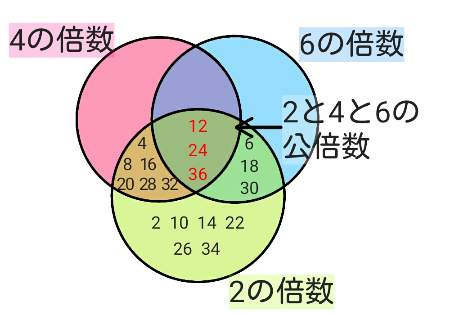
3つ以上の数の最大公約数と最小公倍数も、すだれ算で求めることができます。
まずは最大公約数です。
ここでは、12と18と24の最大公約数を求めてみます。
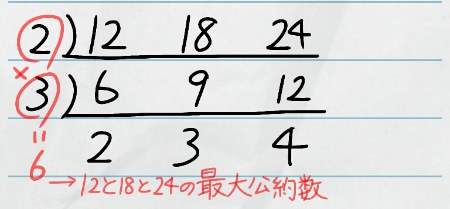
3つの数が共通して割り切れる数で割っていきます。
2・3・4は同じ数で割り切れないのでここですだれ算は終了、2つの数の時と同じく左の数を掛けると、3つの数の最大公約数が求められます。
続いて最小公倍数ですが、これは計算の仕方が少し違ってきます。
では、9と12と18の最小公倍数を求めてみましょう。
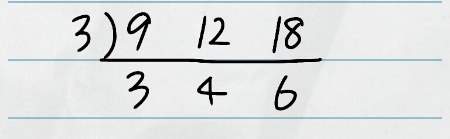
まずは今まで通り、3つの数を共通して割ることができる数を探して割っていきます。
計算を進めていくと、3・4・6となりました。
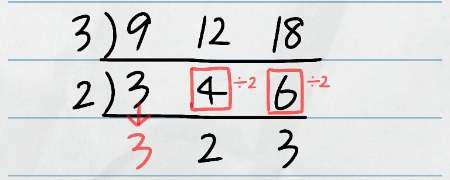
今までの流れだと、これらの数を割ることができる共通の数がないのでここで計算終了となるのですが、3つ以上の数の最小公倍数を求める場合は、2つの数だけで割り切れる場合も計算を進めていきます。
この問題では、「4」と「6」を2で割り切ることができますし、「3」と「6」を3で割り切ることもできます。
どちらでも良いのですが、今回は「4」と「6」を2で割ります。
この時、2で割り切ることのできない「3」はそのまま下に移動させるのがポイントです。
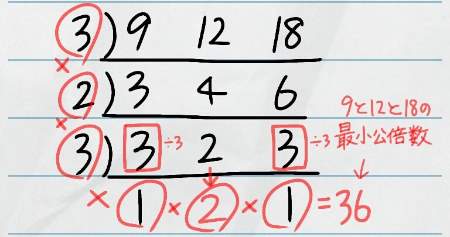
計算の結果、1・2・1となりました。
これらの数は2つだけでももう割ることはできないので、ここでやっとすだれ算は終了です。
後は、2つの数の時と同じようにL字型に掛け算をすれば最小公倍数を求めることができます。
2つの数の場合は同じすだれ算で最大公約数と最小公倍数を求めることができますが、3つ以上の場合は最大公約数と最小公倍数、別々にすだれ算をしなくてはなりません。
混同しないように気を付けましょう。
すだれ算で最大公約数と最小公倍数を求める際の注意点
簡単便利なすだれ算ですが、たかが筆算と思ってはいけません。
先ほど素因数分解の項でもお話ししましたが、計算ミスはかなり痛いです。
例えば、割り算を繰り返した結果「26」と「39」になったとします。
「3…でも割れないなぁ。これで終わり!」と思ってしまいがちですが、冷静に見るとどちらも13で割ることができます。
素因数分解もそうですが、とにかく「まだ計算できないか確認する」ことが大切です。
また、すだれ算を正確に終えても、最後の掛け算で最大公約数を求めるやり方と最小公倍数を求めるやり方を取り違えてしまうこともあります。
どちらもあり得ない感じがしますが、みんなやります。
私もやりました。
次は我が身です…。
大きな証明問題を一生懸命解いても、最初の段階で計算ミスがあれば全て水の泡です。
問題をこなして、落ち着いて解けるようにしましょう。
まとめ
- これ以上割り切れない数を素数と言い、ある数を素数に分けることを素因数分解といいます
- すだれ算を使うと簡単に素因数分解することができます
- 2つ以上の自然数に共通な約数を公約数、倍数を公倍数と言います
- 2つの数は、同じすだれ算で最大公約数と最小公倍数を求めることができます
すだれ算についてご紹介しました。
冒頭にお話ししたとおり、私は高校でこの計算方法を初めて知り、それまですだれ算の存在すら知りませんでした。
もっと早く知りたかったです。
地道に計算するよりも早くて正確なので、すだれ算を使うと便利な場面がたくさん出てきます。
小学生のうちに会得しておくとこの先とても役に立ちますし、中学生の勉強では結構使うと思います。
数が大きくなってくるとユークリッドの互除法を使わなくてなりませんが、やはりすだれ算の手軽さにはかないません。
慣れればとても簡単なので、ぜひ使ってみてくださいね。
